本記事では分離拡大の中間体に関する基本的な性質を解説します。
性質
主張は以下の通りです。
\(L/K\)を体の拡大、\(M,E,F\)をその中間体とし、\(EF\)を\(E\)と\(F\)の合成体とする。このとき以下が成立する。\begin{align}&(1)\;L/K\text{は分離拡大}\Leftrightarrow L/M,M/K\text{はともに分離拡大}\\[10pt]&(2)\;E/K\text{は分離拡大}\Rightarrow EF/F\text{は分離拡大}\\[10pt]&(3)\;E/K,F/K\text{は分離拡大}\Leftrightarrow EF/K\text{は分離拡大}\end{align}
代数拡大についても同じような性質がありましたね。図示すると以下のようになります。
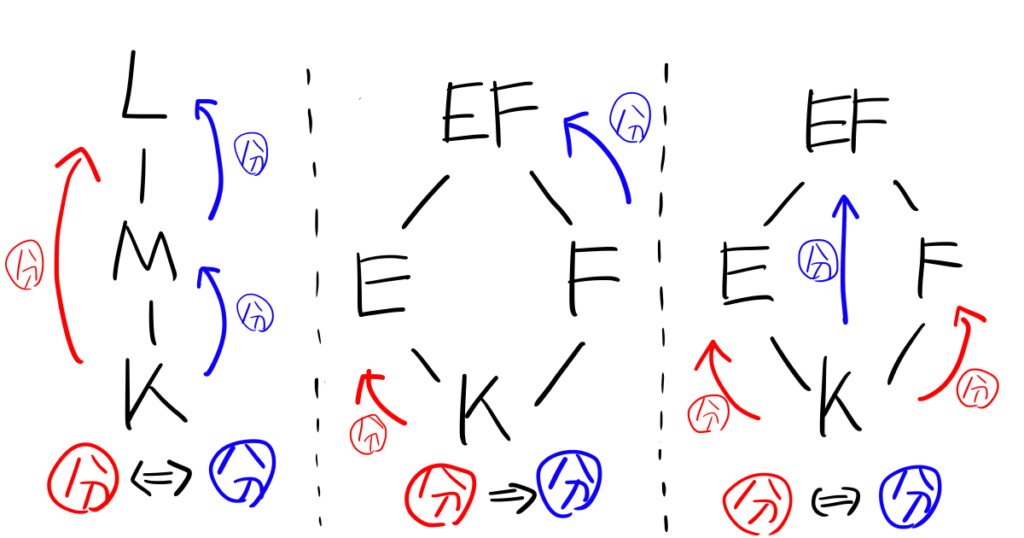
分離拡大の定義については以下の記事で紹介していますので、確認のためにも是非ご覧ください。
証明
地道にひたすら証明していきます。証明中の赤線部分では、以下の記事で紹介している分離拡大の条件を用いているので、こちらもご覧ください。
(1)
(\(\Rightarrow\))\(L/K\)が分離拡大より特にそれは代数拡大なので、代数拡大の性質から\(L/M,M/K\)はともに代数拡大である。
\(x\in L\)とし、\(x\)の\(M,K\)上の最小多項式をそれぞれ\(f_M(X),f_K(X)\)とする。\(L/K\)は分離拡大なので、\(f_K(X)\)は重根を持たない。いま\(f_K(X)\)は\(f_M(X)\)で割り切れるので、\(f_M(X)\)もまた重根を持たない。従って\(L/M\)は分離拡大である。
また\(y\in M\)とし、その\(K\)の最小多項式を\(f(X)\)とする。\(y\)は\(L\)の元でもあり、\(L/K\)が分離拡大であることから\(f(X)\)は重根を持たないことが従う。よって\(M/K\)は分離拡大である。
(\(\Leftarrow\))\(x\)の\(M\)上の最小多項式を\[f(X)=X^n+a_{n-1}X^{n-1}+\cdots+a_0\quad(a_i\in M)\]とすると、\(f(X)\)は分離多項式である。\(K’:=K(a_0,\dots,a_{n-1}),K” :=K'(x)=K(a_0,\dots,a_{n-1},x)\)とおく。\(K’\)は分離拡大\(M/K\)の中間体なので、\(K’/K\)は有限次分離拡大である。\(x\)の\(K’\)上の最小多項式は\(f(X)\)に他ならないので、\(x\)は\(K’\)上分離的。従って\(K” /K’\)も有限次分離拡大となる。よって\begin{align}[K”:K]&=[K”:K’][K’:K]\\&=[K”:K’]_s[K’:K]_s\\&=[K”:K]_s\end{align}が成立するので\(K”/K\)は分離拡大であり、特に\(x\)は\(K\)上分離的となる。従って\(L/K\)は分離拡大である。
(2)\(x\in EF\)とすると、\(x\)は\[x=a_1b_1+\cdots+a_nb_n\quad(a_i\in E,b_i\in F)\]と表せる。いま\(E/K\):分離拡大より各\(a_i\)は\(K\)上分離的なので、特に\(F\)上も分離的である。よって\(F’:=F(a_1,\dots,a_n)\)とおくと\(F’/F\)は有限次分離拡大となる。いま定義から\(x\in F’\)なので、\(x\)は\(F\)上分離的である。従って\(EF/F\)は分離拡大である。
(3)
(\(\Rightarrow\))\(E/K\)は分離拡大なので、(2)から\(EF/F\)は分離拡大である。それと\(F/K\)が分離拡大であることを合わせて、(1)から\(EF/K\)は分離拡大である。
(\(\Leftarrow\))\(E,F\)は\(EF/K\)の中間体なので、(1)が適用でき\(E/K,F/K\)は分離拡大となる。
(証明終)





コメント