環の局所化の普遍性 - 数学をやろう！

本記事では環の局所化の普遍性について解説します。

定義
普遍性
局所化の特徴づけ

定義

局所化の定義については以下の記事で解説しているので、確認のためにもぜひご覧ください。

普遍性

局所化の普遍性とは、以下のような性質です。

$A$を可換環、$S\subset A$を積閉集合とする。$A_S$を$A$の$S$による局所化とし、$i:A\to A_S$を自然な準同型とする。
この時、可換環$B$と環準同型$\phi : A\to B$であって、$$s\in S\Rightarrow \phi(s)\in B^{\times}$$を満たすものに対し、$\phi=\psi\circ i$なる環準同型$\psi:A_S\to B$が一意に存在する。

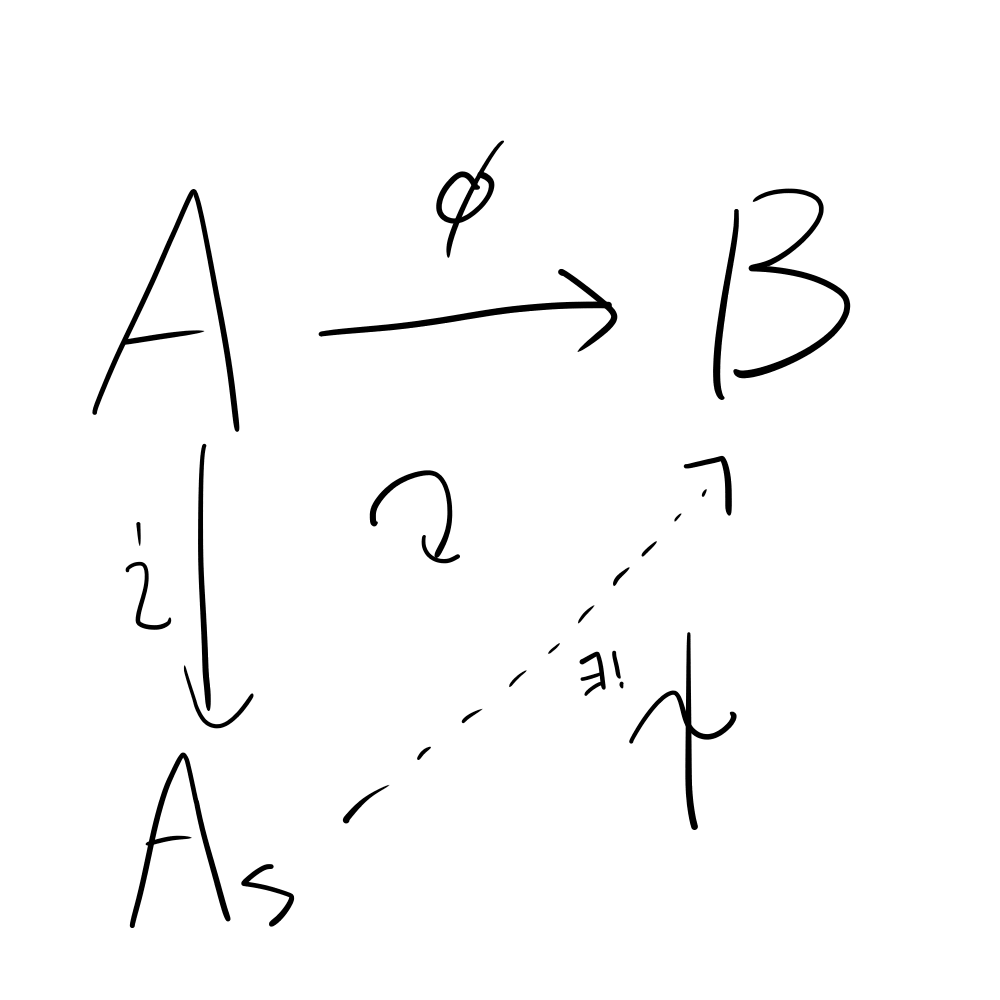
大雑把にいうと、$S$の元が単元に行くようなペア$(B,\phi)$の中で、$(A_S,i)$が最も基本的なものだということです。

(証明)
$a/b\in A_S$に対し、$\psi(a/b):=\phi(a)\phi(b)^{-1}$と定めればよい。
(well-definedness)
$a/b=c/d\in A_S$とすると定義よりある$s\in S$が存在し、$$s(ad-bc)=0\in A$$となる。よって\begin{align}\phi(s)\phi(a)\phi(d)&=\phi(sad)\\&=\phi(sbc)\\&=\phi(s)\phi(b)\phi(c)\end{align}となり、$b,d,s\in S$より$\phi(b),\phi(d),\phi(s)\in B^{\times}$なので、これらの逆元を辺々かけて、$$\phi(a)\phi(b)^{-1}=\phi(c)\phi(d)^{-1}$$となる。よって$\psi$はwell-definedである。

$a\in A$に対し$$\psi(i(a))=\psi \left( \frac{a}{1}\right)=\phi(a)$$より$\phi=\psi\circ i$が成り立つ。
最後に一意性を示す。$\phi=\psi’\circ i$なる別の準同型$\psi’:A_S\to B$と任意の$a/b\in A_S$に対し、\begin{align}\phi(b)\psi’\left(\frac{a}{b}\right)&=\psi’\left(\frac{b}{1}\right)\psi’\left(\frac{a}{b}\right)\\&=\psi’\left(\frac{a}{1}\right)\\&=\psi'(i(a))\\&=\phi(a)\end{align}となり、$b\in S$より$\phi(b)\in B^{\times}$なので、$\phi(b)^{-1}$を両辺にかけることで$$\psi’\left(\frac{a}{b}\right)=\phi(a)\phi(b)^{-1}=\psi\left(\frac{a}{b}\right)$$を得る。よって$\psi=\psi’$
(証明終)

局所化の特徴づけ

実はこの普遍性が局所化の特徴づけになっていることが示せます。

可換環$C$と環準同型$j:A\to C$が$$j(s)\in C^{\times}(\forall s\in S)$$と上の普遍性を満たしたとする。すなわち可換環$B$と環準同型$\phi : A\to B$であって、$$s\in S\Rightarrow \phi(s)\in B^{\times}$$を満たすものに対し、$\phi=\psi\circ j$なる環準同型$\psi:C\to B$が一意に存在するとする。この時、$C$は$A_S$と同型となる:$$C\cong A_S$$

普遍性を満たすものは同型を除いて一意に存在し、それは局所化によって与えられるということです。
この事実があるので、本や先生によっては局所化を普遍性によって定義している場合もあります。

(証明)
上の普遍性において$B:=A_S,\phi:=i:A\to A_S$とおくことで$i=\psi\circ j$なる環準同型$\psi:C\to A_S$が一意にとれる。一方$A_S$の普遍性において$B:=C,\phi:=j:A\to C$とおくことで、$j=\psi’\circ i$なる環準同型$\psi’:A_S\to C$が一意にとれる。このとき、$$\psi\circ\psi’\circ i=\psi\circ j=i$$より、下の(図1)は可換。
ところで$A_S$の普遍性において$B:=A_S,\phi=i$とすると、$i=\lambda\circ i$なる環準同型$\lambda:A_S\to A_S$が一意にとれるが、$\lambda$として恒等写像$\mathrm{id}_{A_S}$をとればよいことは明らか(図2)。よって$\lambda$の一意性から、$$\psi\circ\psi’=\lambda=\mathrm{id}_{A_S}$$が成立する。同様にして$$\psi’\circ\psi=\mathrm{id}_A$$が分かるので、$\phi$と$\psi$は互いに逆写像を与えており、これらが同型写像なことが示せた。
(証明終)

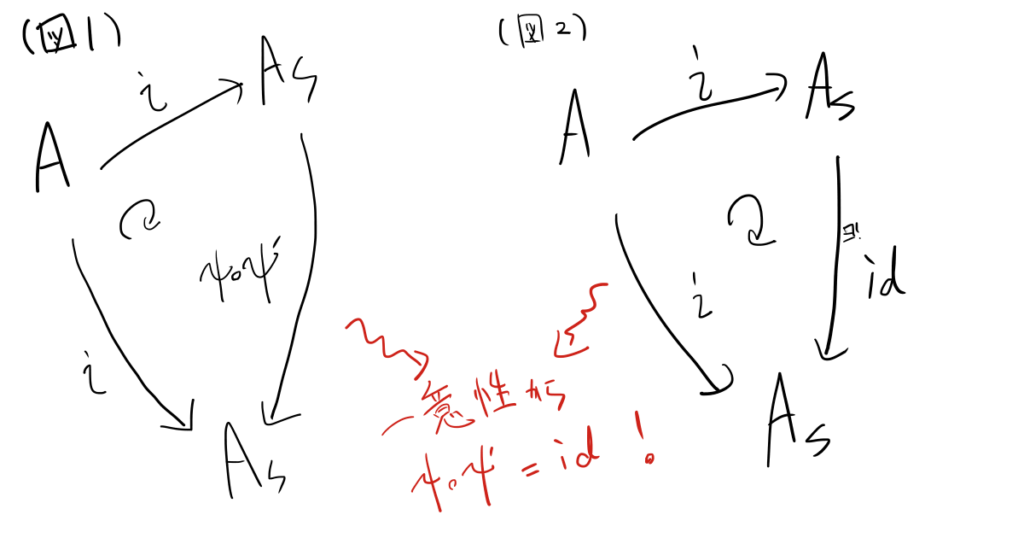
普遍性を用いた証明は形式的なものになりがちで慣れるまでは難しいかもしれませんが、随所で用いるので練習してみるといいかもしれません。