本記事では局所化の剰余環について紹介します。
主張
\(A\)を可換環、\(S\subset A\)を積閉集合、\(A_S\)を\(A\)の\(S\)による局所化とする。\(I\subset A\)をイデアルとしたとき、以下の同型が存在する。$$A_S/ IA_S \cong (A/I)_{\bar{S}}$$ここで\(\bar{S}\)とは自然な全射\(A\to A/I\)による\(S\)の像のこと。
つまり「局所化してからイデアルで割る」のと、「イデアルで割ってから局所化する」のは同じことだと言っているのです。
証明
愚直に同型写像を構成します。局所化の普遍性をもりもり使うので、必要なら以下の記事で確認してください。
自然な環準同型\(A\to A_S\)と自然な全射\(A_S\to A_S/IA_S\)を合成することで、環準同型$$\phi:A\to A_S/IA_S\;;\;a\mapsto \overline{\left(\frac{a}{1}\right)}$$が定まる。ここで\(a\in I\)に対し、$$\phi(a)=\overline{\left(\frac{a}{1}\right)}=0$$より\(\phi\)は$$\bar{\phi}:A/I\to A_S/IA_S\;;\;\bar{a}\mapsto \overline{\left(\frac{a}{1}\right)}$$を誘導する。さらに\(s\in S\)に対し\(s/1\in A_S^{\times}\)より、\(\overline{s/1}\in (A_S/IA_S)^{\times}\)となる(※単元の像は単元である)。従って局所化の普遍性から、\(\bar{\phi}\)は環準同型$$\Phi:(A/I)_{\bar{S}}\to A_S/IA_S\;;\;\frac{\bar{a}}{\bar{b}}\mapsto \overline{\left(\frac{a}{b}\right)}$$を誘導する。
一方、自然な全射\(A\to A/I\)と自然な環準同型\(A/I\to (A/I)_{\bar{S}}\)を合成することで、環準同型$$\psi:A\to (A/I)_{\bar{S}}\;;\;a\mapsto \frac{\bar{a}}{1}$$が定まる。ここで\(s\in S\)に対し、\(\overline{s}/1\in (A/I)_{\bar{S}}^{\times}\)ゆえ、局所化の普遍性から\(\psi\)は$$\psi’:A_S\to (A/I)_{\bar{S}}\;;\;\frac{a}{b}\mapsto \frac{\bar{a}}{\bar{b}}$$を誘導する。さらに\(a/b\in IA_S\:\)(すなわち\(a\in I\))に対し、$$\psi’\left(\frac{a}{b}\right)=\frac{\bar{a}}{\bar{b}}=0$$より、\(\psi’\)は環準同型$$\Psi:A_S/IA_S\to (A/I)_{\bar{S}}\;;\;\overline{\left(\frac{a}{b}\right)}\mapsto \frac{\bar{a}}{\bar{b}}$$を誘導する。これら\(\Phi\)と\(\Psi\)が互いに逆写像となっているのは明らかなので、これが同型$$A_S/ IA_S \cong (A/I)_{\bar{S}}$$を与える同型写像となる。
(証明終)
特別な場合
素イデアルによる局所化の場合を考えてみましょう。
素イデアル\(p\subset A\)に対し、\(S=A\backslash\; p\)として上の性質を適用すると、$$\bar{S}=A/p\;\backslash\{0\}$$となることより、以下を得る。$$A_p/pA_p\cong \mathrm{Frac}(A/p)$$
こういう二つの操作が可換になる感じの性質、嬉しいですね。まあ局所化も剰余を取るのも同値関係で割っているという意味では同じ操作なので、成り立ってしかるべきとも言えるかもしれませんが……
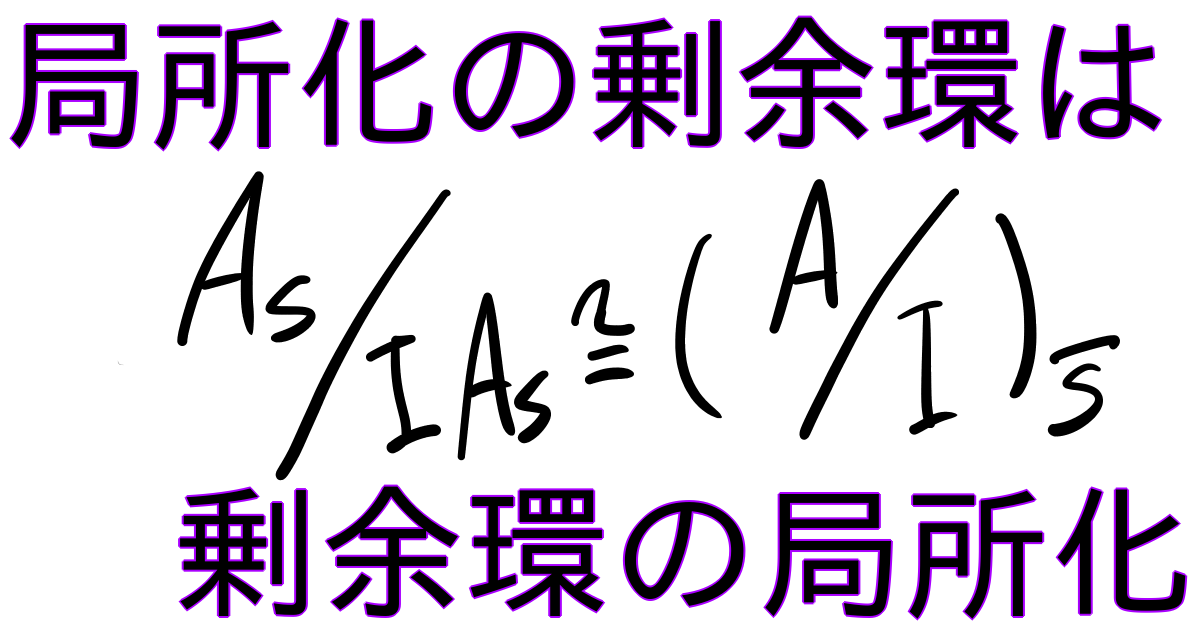



コメント