本記事ではガロア拡大について解説します。言わずと知れたガロア理論の世界への第一歩ですので、しっかり理解しておきましょう!
定義
定義は以下の通りです。
分離的かつ正規な体拡大をガロア拡大と呼ぶ。
また\(L/K\)をガロア拡大としたとき、\[\mathrm{Gal}(L/K):=\mathrm{Aut}(L/K)\]を\(L/K\)のガロア群と呼ぶ。
二つの良い性質を併せ持つ体拡大ということです。分離拡大、正規拡大についてはそれぞれ以下の記事で解説しています。
例
いくつか例を見てみましょう。簡単のためにまずは\(\mathbb{Q}\)の拡大を考えてみます。\(\mathbb{Q}\)は標数\(0\)の体なので、その代数拡大は自動的に分離拡大となります(このような性質をもつ体を完全体と呼びます)。なので、\(\mathbb{Q}\)のガロア拡大とは正規拡大のことに他なりません。なので正規拡大の記事で例として挙げている、\[\mathbb{Q}(\sqrt2)/\mathbb{Q}\;,\;\overline{\mathbb{Q}}/\mathbb{Q}\] などはガロア拡大となります(\(\overline{\mathbb{Q}}\)は\(\mathbb{Q}\)の代数閉包)。
一方で、正規拡大でない \[\mathbb{Q}(\sqrt[3]2)/\mathbb{Q}\] は分離拡大ではありますが、ガロア拡大ではありません。
次に標数\(p>0\)の体の例を見てみましょう。有限体の拡大\[\mathbb{F}_{p^n}/\mathbb{F}_p\]は、\(\mathbb{F}_p\) が完全体であることから分離拡大です。また、\(\mathbb{F}_{p^n}\) は \(X^{p^n}-X\in \mathbb{F}_p[X]\) の最小分解体として与えられていたので、これは正規拡大でもあります。
以上より拡大 \(\mathbb{F}_{p^n}/\mathbb{F}_p\) はガロア拡大です。
一方で、非分離拡大の典型例\[\mathbb{F}_p(T)/\mathbb{F}_p(T^p)\]は、生成元\(T\)の最小多項式が \(X^p-T^p\) で与えられることから、\(T\)の共役元は\(T\)自身のみであることが分かるので正規拡大ではありますが、ガロア拡大ではありません。
性質
ガロア拡大には中間体に関して次のような性質を持ちます。
\(L/K\)を体の拡大、\(M,E,F\)をその中間体とし、\(EF\)を\(E\)と\(F\)の合成体とする。このとき以下が成立する。\begin{align}&(1)\;L/K\text{はガロア拡大}\Rightarrow L/M\text{はガロア拡大}\\[10pt]&(2)\;E/K\text{はガロア拡大}\Rightarrow EF/F\text{はガロア拡大}\\[10pt]&(3)\;E/K,F/K\text{はガロア拡大}\Rightarrow EF/K\text{はガロア拡大}\end{align}
図示すると以下の通りです。
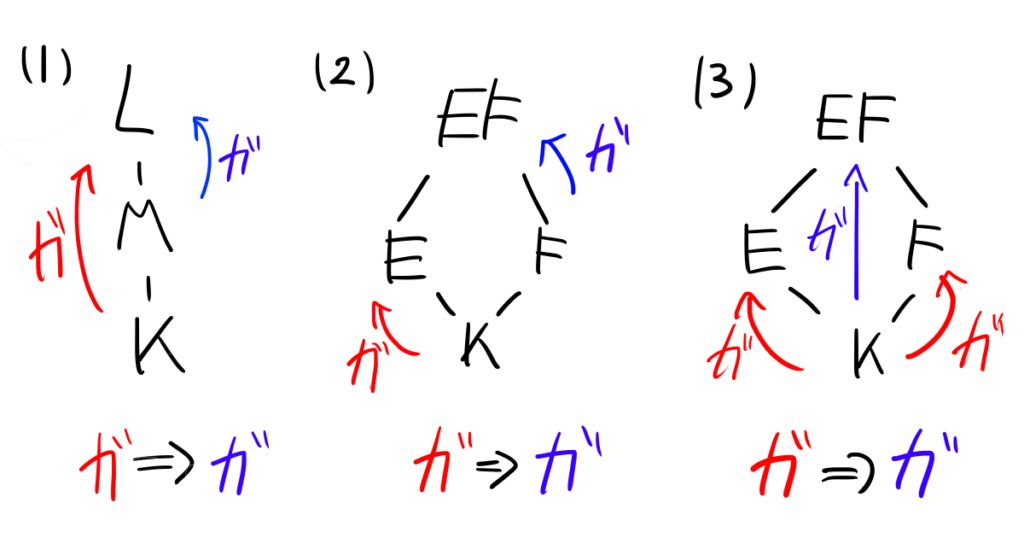
(1)はガロアの基本定理へ、(2),(3)は推進定理へと繋がる重要な性質です。
証明
証明は正規拡大と分離拡大の中間体に関する同様の性質をくっつけて行います。具体的にはそれぞれ以下のような性質を持つのでした。
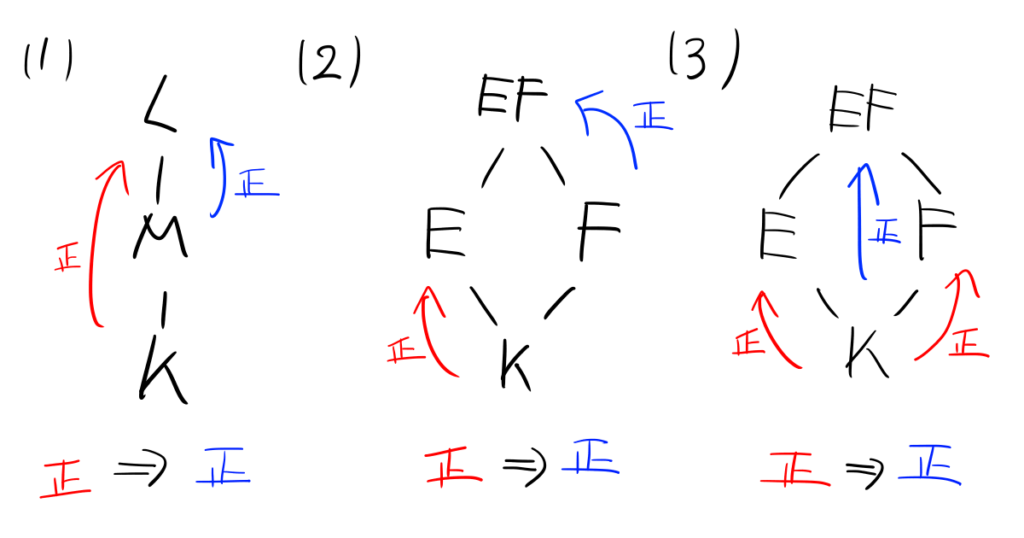
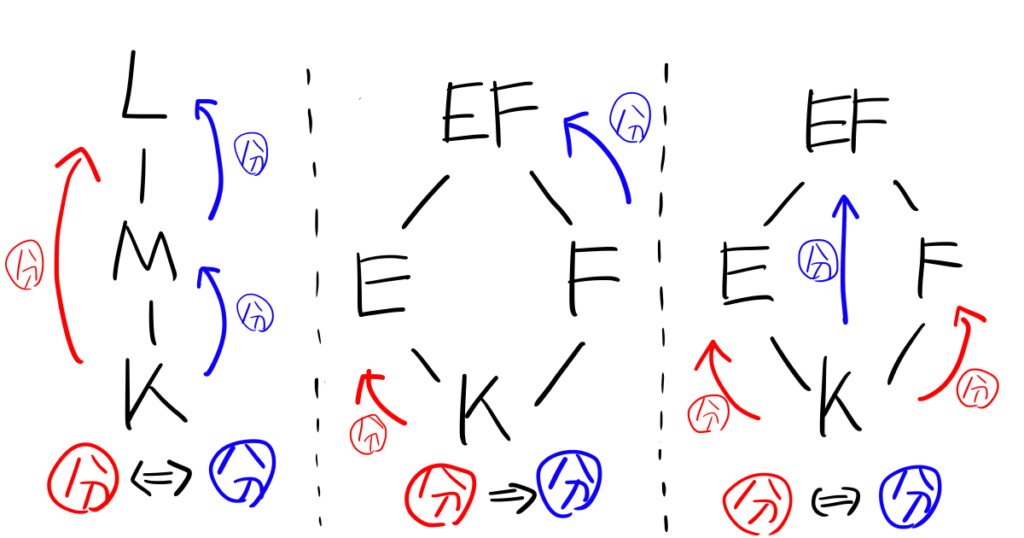
それぞれ以下の記事で証明しているので、よろしければご覧ください。
見ての通り正規拡大の性質の方が、分離拡大のそれより真に弱くなっています。なのでガロア拡大については正規拡大とまったく同様の性質が成立することがわかります。
(証明終)
最後に
本記事ではガロア拡大の定義と例、基本的な性質について解説しました。ガロア拡大の定義には同値な言いかえがいくつも存在します。その辺りについては以下の記事で解説しています。
また、ガロア理論の集大成といえば”ガロアの基本定理”ですが、こちらも以下の記事で解説しています。









コメント