体の拡大 | 言葉の定義とその種類

本記事では体の拡大について基本的な定義を紹介した後、特に大事な拡大をまとめています。ガロア理論などに興味のある方には必須の知識となるので、ここで確認しておきましょう！

定義
拡大次数
拡大の種類
それぞれの関係

定義

まずは体の拡大についてです。

$K,L$を$K\subset L$なる体で、これらの演算が一致している(つまり$L$の演算の$K$への制限が$K$の演算となっている)とき、$K$を$L$の部分体、$L$を$K$の拡大体と呼ぶ。
$L$が$K$の拡大体であることを$L/K$のように表す。

$L$の部分体で$K$の拡大体となっている体$M$のことを拡大$L/K$の中間体と呼び、$L/M/K$と表す。

分かりやすい例としては$\mathbb{C}/\mathbb{R}/\mathbb{Q}$などがありますね。また、体の拡大を図式を使って下図のように線で結んで表すことがよくあります。下が部分体で、上が拡大体です。

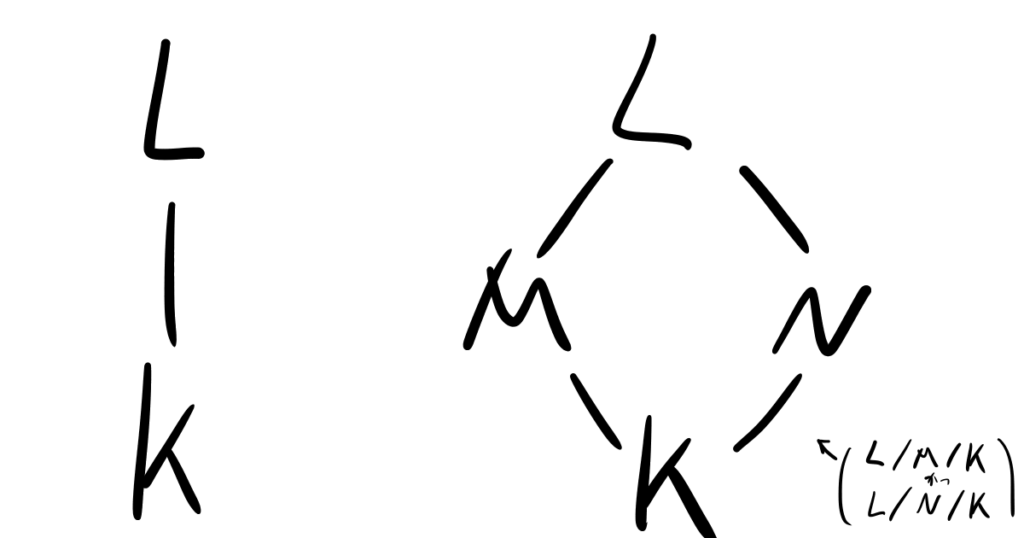
拡大次数

次に拡大次数の定義です。

$L/K$を体の拡大とする。このとき、$L$は$K$上のベクトル空間となり、その次元を$L/K$の拡大次数と呼び、[$L:K$]と表す。$$[L:K]:=\mathrm{dim}_K L$$
ただし$L$が$K$上無限次元のときは$[L:K]=\infty$と表すことにする。

例えば$\mathbb{C}/\mathbb{R}$の例では、$\mathbb{C}\cong\mathbb{R}^2$なので[$\mathbb{C}:\mathbb{R}$]=2ですね。

ここで、拡大次数に関する基本的な性質を見ておきましょう。

$L/M/K$を体の拡大の列とする。このとき、以下の等式が成立する。$$[L:M][M:K]=[L:K]$$
両辺共に$\infty$となる場合も含む。

体の拡大を考えるにあたって極めて基本的な等式です。使いこなせるようにしておきましょう。

(証明)まず$[L:M], [M:K]<\infty$の場合を考える。$[L:M]=n, [M:K]=m$とおくと、拡大次数の定義から、$L$の$M$上の基底$E=\{e_1, \dots e_n\}$と、$M$の$K$上の基底$F=\{f_1, \dots f_m\}$が取れる。このとき、$mn$個の元$$e_if_j\:(i=1,\dots n,j=1,\dots m)$$が$L$の$K$上の基底をなすことを示す。
($L$を張ること)
$x\in L$を任意に取る。いま$E$は$L$の$M$上の基底なので、ある$y_i\in M$を用いて$$x=\sum_{i=1}^ny_ie_i$$と表せる。さらに$F$が$M$の$K$上の基底であることから、ある$c_{ij}\in K$を用いて$$y_i=\sum_{j=1}^mc_{ij}f_j$$と表せる。これを上の式に代入して、\begin{align}x&=\sum_{i=1}^ny_ie_i\\&=\sum_{i=1}^n\left(\sum_{j=1}^mc_{ij}f_j\right)e_i\\&=\sum_{i,j}c_{ij}e_if_j\end{align}となる。よって$\{e_if_j\}_{i,j}$は$K$上$L$を張ることが分かった。
(一次独立性)$$\sum_{i,j}c_{ij}e_if_j=0\:\:(c_{ij}\in K)$$とする。このとき$c_{ij}=0\:(\forall i,j)$を示せばよい。上式を変形すると、\begin{align}\sum_{i,j}c_{ij}e_if_j&=\sum_{i=1}^n\left(\sum_{j=1}^mc_{ij}f_j\right)e_i\\&=0\end{align}となる。いま$E$は$M$上一次独立なので、$i=1,\dots n$に対して$$\sum_{j=1}^mc_{ij}f_j=0$$が従う。さらに$F$が$K$上一次独立であることから結局$$c_{ij}=0(\forall i,j)$$となり、$\{e_if_j\}_{i,j}$が$K$上一次独立であることが示せた。

以上より$\{e_if_j\}_{i,j}$は$L$の$K$上の基底となり、$[L:K]=mn=[L:M][M:K]$が従う。

次に無限大が絡む場合について、上の証明から$$[L:M], [M:K]<\infty\Rightarrow[L:K]<\infty$$が分かる。対偶を考えることにより、$$[L:K]=\infty\Rightarrow “[L:M]=\infty または [M:K]=\infty”$$となり両辺ともに無限大で等式が成立することが分かる。よって残りは左辺が無限大すなわち$“[L:M]=\infty$ または $[M:K]=\infty”$のとき、$[L:K]=\infty$となり等式が成立することを示せばよい。これも対偶を示すため、$[L:K]<\infty$と仮定する。このとき$M$は$L$の部分$K$-ベクトル空間なので、$$[M:K]\leq [L:K]<\infty $$が従う。さらに$L$の$K$上の基底を$E=\{e_1,\dots e_n\}$とする。このとき$$L=\mathrm{span}_KE\subset \mathrm{span}_ME\subset L$$より、$\mathrm{span}_ME=L$すなわち$E$が$M$上$L$を張ることが分かる。よって$E$の部分集合$E’$で、$L$の$M$上の基底となるものが存在する。従って$[L:M]=|E’|\leq |E|<\infty$となる。

(証明終)

拡大の種類

いろいろな種類の拡大があるので、以下にまとめてみました。

有限次拡大, 無限次拡大

$[L:K]<\infty$なる拡大$L/K$を有限次拡大と呼び、そうでないとき無限次拡大と呼ぶ。

単拡大

ある$a\in L$によって$L=K(a)$と表せるとき、拡大$L/K$を単拡大と呼ぶ。

代数拡大, 超越拡大

任意の$x\in L$が$K$上代数的な時、拡大$L/K$を代数拡大と呼び、そうでないとき超越拡大と呼ぶ。

代数拡大については以下の記事で詳しく解説しています。

正規拡大

$L/K$を代数拡大とする。任意の$x\in L$に対し、$x$の$K$上の最小多項式$f(X)\in K[X]$が$L[X]$の中で一次式の積に分解できる、すなわち$$f(X)=c(X-\alpha_1)\cdots (X-\alpha_n) \:\:(\alpha_i\in L)$$と表せるとき、拡大$L/K$を正規拡大と呼ぶ。

正規拡大については以下の記事で詳しく解説しています。

分離拡大

$L/K$を代数拡大とする。任意の$x\in L$が$K$上分離的なとき、$L/K$を分離拡大と呼ぶ。

分離拡大については以下の記事で詳しく解説しています。

純非分離拡大

$L/K$を代数拡大とする。任意の$a\in L\backslash K$が$K$上分離的でないとき、$L/K$は純非分離拡大であるという。

純非分離拡大については以下の記事で詳しく解説しています。

ガロア拡大

正規かつ分離的な拡大をガロア拡大と呼ぶ。

ガロア拡大については以下の記事で詳しく解説しています。

それぞれの関係

有限生成代数拡大$\iff$有限次拡大
有限次分離拡大$\Rightarrow$単拡大　(原始元定理)