本記事では環の標数の定義について解説します。
定義
定義は以下の通りです。
\(A\) を環、\(0_A\in A\) をその加法単位元、\(1_A\in A\) をその乗法単位元とする。このとき正整数\(n>0\)に対し、\(1_A\) を\(n\)個足し合わせたものを \(n_A\) とする:\[n_A:=1_A+\cdots+1_A\]この上で、\[n_A=0_A\]となる\(n\)が存在する場合、その中で最小のものを\(A\)の標数と呼び、\[\text{ch} A\]と表す。またそのような\(n\)が存在しない場合、\(A\)の標数は\(0\)であると定める:\[\text{ch}A:=0\;\stackrel{\mathrm{def}}{\Longleftrightarrow}\;n_A\neq0\;(\forall n>0)\]
\(1\)を足していって\(0\)になる……?少し変な感じですが、まずは例を見てみましょう。
例
まずは環といったら真っ先に思い浮かぶ、整数環 \(\mathbb{Z}\) について考えてみましょう。
……とはいっても、どう考えても\(1\)を足していって\(0\)になるなんてことはありませんね。つまり \(\mathbb{Z}\) は標数\(0\)の環だということです。
では標数が正となる環とはどのようなものでしょうか。典型的な例は \(\mathbb{Z}\) の剰余環です。
\(R=\mathbb{Z}/2\mathbb{Z}\) の場合を考えてみましょう。これは位数\(2\)の環であり、ここでは\[\mathbb{Z}/2\mathbb{Z}=\left\{\overline0,\overline1\right\}\]とおいておきます。もちろん\(\overline0\)が加法単位元で、\(\overline 1\)が乗法単位元です。このときご存知の通り、\[2_R=\overline1+\overline1=\overline0\]が成立します。また、当然 \(\mathbb{Z}/2\mathbb{Z}\) は零環ではないので、\[\overline1\neq\overline0\]です。従って\(n=2\)が\[n_R=0\]となる最小の正整数なので、\[\text{ch}(\mathbb{Z}/2\mathbb{Z})=2\]が従います。同様に考えて、正整数\(n>0\)に対し\[\text{ch}(\mathbb{Z}/n\mathbb{Z})=n\]となります。
性質
ここで一つ性質を見ておきましょう。
\(A,B\) を環とする。これらの間に単射環準同型\[f:A\to B\]が存在するなら、\(\text{ch}A=\text{ch}B\) が成立する。
(証明)\(f:A\to B\) が単射であることと\[x=0_A\Leftrightarrow f(x)=0_B\]となることが同値であることに注意しておく。これを踏まえると、\begin{align}n_A=0_A&\Leftrightarrow f(n_A)=0_B\\[5pt]&\Leftrightarrow n_B\cdot f(1_A)=0_B\\[5pt]&\Leftrightarrow n_B\cdot 1_B=0\\[5pt]&\Leftrightarrow n_B=0_B\end{align}となる。よって\[\text{ch}A=\text{ch}B\]が成立する。
(証明終)
この対偶を考えると、以下のようになりますね。
標数の異なる環の間には単射環準同型は存在しない。
写像の存在に制限を与えるという意味で、標数は環の構造にクリティカルに関わってくる量だということです。
体について
ここまでは一般の環について話をしてきましたが、標数は体に対して考えられることが多い概念です。その理由の一つが、先に述べた準同型の存在との関係です。
まず思い出してほしいのが、体の間の環準同型は自動的に単射になるという事実です。これと上で見た性質を合わせると、次のことが分かります。
\(K,L\)を体とする。これらの間に環準同型\[K\to L\]が存在するなら、\(\text{ch}K=\text{ch}L\) が成立する。
言い換えれば、標数の異なる体の間に環準同型は存在しない。
現代数学の多くの分野は、そこで扱う”対象”(環やベクトル空間、位相空間など)と、その最低限の構造を保つ”写像”(環準同型や線型写像、連続写像など)によって構成されています。例えば環について調べたいのに、その環としての構造(各種単位元や演算など)をガン無視した写像を考えてしまってはあまり意味がありません。
つまり体の構造を考える上では、登場する写像は少なくとも環準同型であってほしいのですが、それは標数が異なると叶わないということです。言い換えれば、体論は標数によって分断されてしまっているということです。
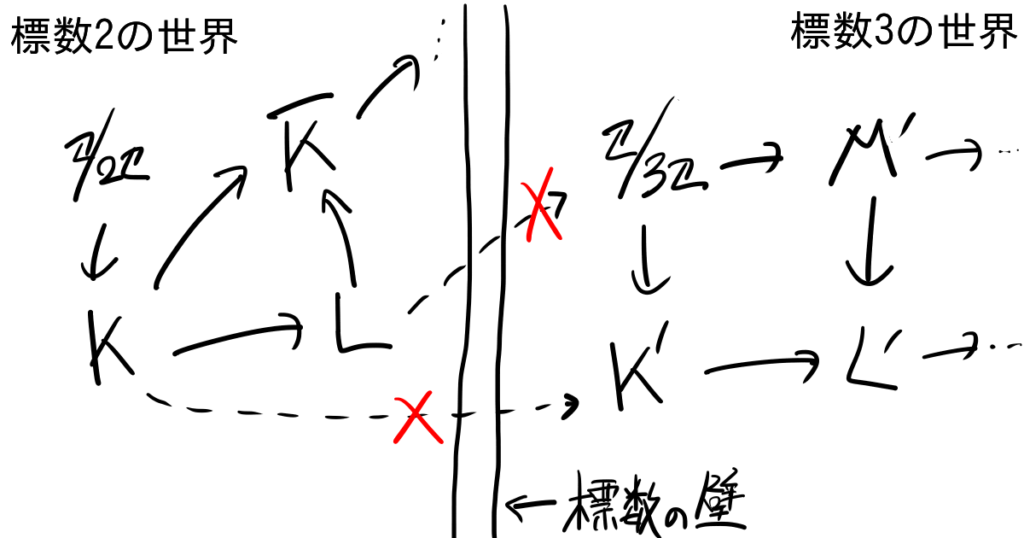
逆に言えば、体論をやる上ではある特定の標数の体についてだけ考えていれば十分だということです。
以上の理由から、とりわけ体論においては標数が重要な存在となっています。以下、体の標数に関する性質を見ていきましょう。
性質(体ver.)
標数が\(0\)の場合と正の場合に分けて性質を見ていきましょう。
性質1
まずは標数が正(これを正標数ともいう)の体についてです。
\(K\) を正標数の体とする。このとき、標数 \(\text{ch}K\) は素数である。
(証明)\(n=\text{ch}K>0\) とおき、これが素数でないと仮定する。このとき\[n=lm\quad(l,m\geq2)\]と分解できる。よって\[0_K=n_K=l_Km_K\]となる(二つ目の等号は両辺ともに \(1_K\) を \(n=lm\) 個足し合わせたものだから)。いま \(K\) は体なので \(l_K=0\) あるいは \(m_K=0\) となる。しかしいま \(l,m<n\) なので、これは標数 \(n\) の最小性に矛盾。よって \(n=\text{ch}K\) は素数である。
(証明終)
性質2
続いて標数\(0\)の体についてです。
標数\(0\)の体は無限体である。さらにそれは有理数体 \(\mathbb{Q}\) を部分体としてもつ。
※このような主張については、少し注意が必要かもしれません。これは実際に \(\mathbb{Q}\) を部分体として含むという意味ではなく、体の埋め込み(要するに単射環準同型)\[i:\mathbb{Q}\hookrightarrow K\]が存在するという意味です。\(i\)による像は実際に \(K\) の部分体であり、\(\mathbb{Q}\) と同型です;\[i:\mathbb{Q}\stackrel{\cong}{\longrightarrow}i(\mathbb{Q})\subset K\]この同型によって部分体 \(i(\mathbb{Q})\) を \(\mathbb{Q}\) と同一視した上で、
\(K\) は \(\mathbb{Q}\) を部分体としてもつ。
といっているわけです。
(証明)\(K\) を標数\(0\)の体とする。このとき対応 \(1\mapsto 1_K\) は環準同型\[i:\mathbb{Z}\to K\]を定める。\(K\) の標数が\(0\)であることから、\[\ker i=\{0\}\]が従う。特に \(n\neq0\) なら\[i(n)\in K\backslash \{0\}=K^{\times}\]となる。よって局所化の普遍性から、\(i\) は環準同型\[\mathrm{Frac}(\mathbb{Z})=\mathbb{Q}\to K\]を誘導する。これは体の間の環準同型なので、体の埋め込みである。従って \(K\) は \(\mathbb{Q}\) を部分体として含む。また無限集合を部分集合に持つということは \(K\) 自身無限体である。
(証明終)
この対偶を考えると次のようになりますね。
有限体は正標数である
また今の性質\(2\)から、\(\mathbb{Q}\) が標数\(0\)の体の中で最小のものだということが分かりました。このような体を素体と呼びます。標数 \(p\) の体についても素体が存在し、実はそれは \(\mathbb{Z}/p\mathbb{Z}\) であることが知られています。素体についてはまた別記事で紹介します。



コメント