本記事ではベズーの等式について解説します。誰もが一度は見たことがあるであろう形の等式を一般化した等式です。
主張
こんな等式のことです。
\(R\) を単項イデアル整域(以下PID)とする。\(a,b\in R\) に対し、\(d=\gcd(a,b)\) を\(a\)と\(b\) の最大公約元とする。このときある \(x,y\in R\) が存在し、\[ax+by=d\]が成立する。
ちょっとピンとこない人もいるかもしれませんね。もう少し特別な場合の例を見てみましょう。
\(R=\mathbb{Z}\) としてみましょう。さらに整数\(a\)と\(b\)は互いに素、すなわち \(\gcd(a,b)=1\) であるとしましょう。このときに上の主張を適用すると、
ある整数\(x,y\in \mathbb{Z}\)が存在し、\[ax+by=1\]が成立する
となります。
どうでしょうか?高校時代に見覚えがある方も多いのではないでしょうか。ユークリッドの互除法を使って導いた、整数問題で頻出のアレです。今回ご紹介するのはこの性質のPIDへの一般化ということです。
証明
では証明しましょう。
(証明) 単項イデアル \((a),(b)\subset R\) を考える。いま \(R\) はPIDなので、\[ (a)+(b)=(d’)\qquad\cdots(\star)\]なる \(d’\in R\) が存在する。ここでまず \(d’\in (a)+(b)\) より\[d’=sa+tb\qquad (s,t\in R)\]と表せる。いま \(d\) は \(a\) と \(b\) の最大公約元なので \(d\mid a,b\) より、\[d\mid d’\]が成立する。一方 \((\star)\) より \(a,b\in (d’)\) となることから\[d’\mid a,\quad d’\mid b\]となる。よって \(d\)が\(a\)と\(b\)の最大公約元であることより、\[d’\mid d\]となる。以上より、\(d’\)は\(d\)の単元倍であることが分かり、特に\[(d’)=(d)\]である。以上より \((a)+(b)=(d)\) が従う。このことから特に、\[d\in (a)+(b)\]すなわちある\(x,y\in R\)が存在し、\[ax+by=d\]が成立する。
(証明終)
この証明の中で示された、イデアルに関する性質を述べておきます。
\(R\)をPIDとする。このとき \(a,b\in R\) に対し、\[(a)+(b)=(\gcd(a,b))\]が成立する。特に以下が同値となる。\begin{align}&(1)\quad aとbは互いに素\\[5pt]&(2)\quad イデアル(a)と(b)は互いに素\end{align}
綺麗でいい感じですね。数学をやっていると、時々このようにすっきりできるタイミングがあるので楽しいです。
一般化
実は元の個数を一般化することができます。
\(R\) をPID、\(a_1,a_2,\dots,a_n\in R\)とし、\(d:=\gcd(a_1,a_2,\dots,a_n)\)とする。このときある\(x_1,x_2,\dots,x_n\in R\)が存在し、\[a_1x_1+a_2x_2+\cdots+a_nx_n=d\]が成立する。
証明は上と全く同様なので割愛します。
まとめ
本記事ではベズーの公式について紹介しました。中高で習った定理がさらに一般化できることを知ることができるのも大学数学の醍醐味ですね。
ちなみにその名の由来となっているベズー(Bèzout)は代数幾何の分野でも重要な「ベズーの定理」でも知られています。
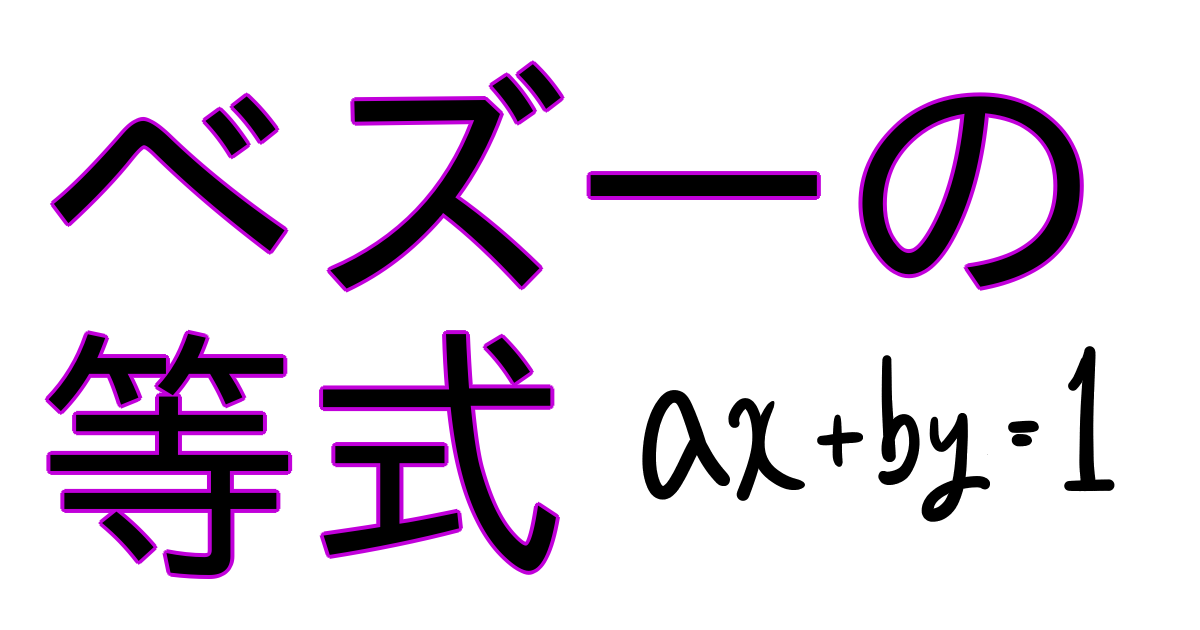


コメント