本記事では代数拡大の中間体、合成体に関する性質を解説します。
主張
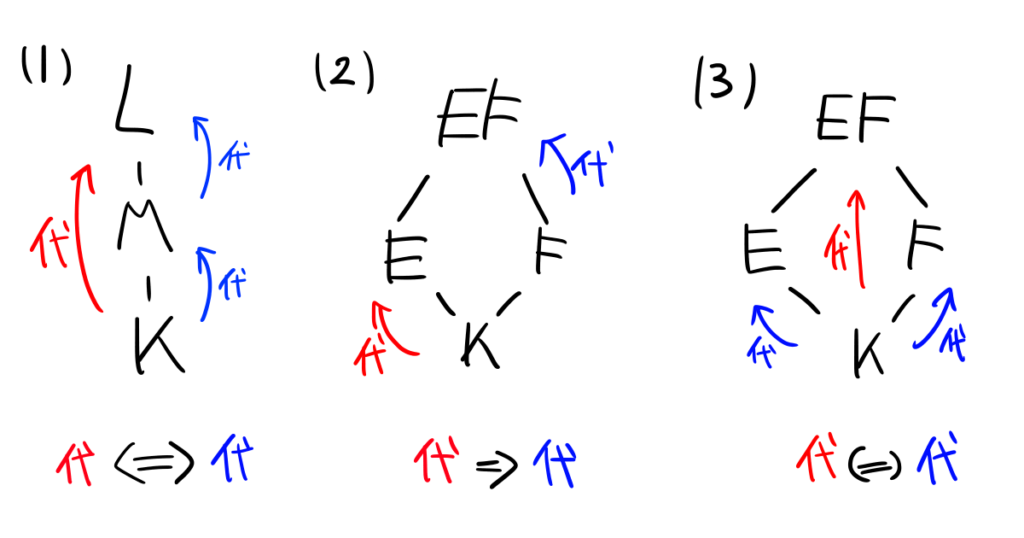
\(L/K\)を体の拡大、\(M,E,F\)をその中間体とし、\(EF\)を\(E\)と\(F\)の合成体とする。このとき以下が成立する。\begin{align}&(1)&L/K\text{は代数拡大}&\Leftrightarrow L/M,M/K\text{はともに代数拡大}\\[10pt]&(2)&E/K\text{は代数拡大}&\Rightarrow EF/F\text{は代数拡大}\\[10pt]&(3)&EF/K\text{は代数拡大}&\Leftrightarrow E/K,F/K\text{はともに代数拡大}\end{align}
図示すると以下のようになります。
証明
基本的には定義通り確認していきます。体論でよくやるように、有限次拡大に帰着して示す部分もあるので、必要ならこちらの記事も参考にしてください。
(証明)
(1)
(\(\Leftarrow\)) \(x\in L\)を任意に取ると、\(L/K\)が代数拡大であることより、ある\(f(X)\in K[X]\)が存在し、\(f(x)=0\)が成立する。ここで\(K\subset M\)より\(f(X)\)は\(M[X]\)の元でもあるので、\(x\)は\(M\)上代数的でもある。よって\(L/M\)は代数拡大。
さらに任意に\(y\in M\)を取る。\(M\subset L\)より\(y\)は\(L\)の元でもあり、\(L/K\)が代数拡大なことにより\(g(X)\in K[X]\)で\(g(y)=0\)なるものが存在する。よって\(y\)は\(K\)上代数的であり、\(M/K\)が代数拡大なことが従う。
(\(\Rightarrow\))\(x\in L\)を任意に取る。\(L/M\)が代数拡大であることより、\(M\)係数多項式$$f(X)=a_nX^n+\dots +a_0\:\:(a_i\in M)$$が存在し\(f(x)=0\)となる。ここで拡大体\(K’:=K(a_0,\dots ,a_n)\)を考える。列\(M/K’/K\)に着目すると、\(M/K\)が代数拡大な事より、\(K’/K\)も代数拡大であることが上で示したことから分かる。よって拡大\(K’/K\)は有限生成な代数拡大となる。従って\(K’/K\)は有限次拡大である(こちらを参照のこと)。同様にいま\(x\)は\(K’\)上代数的なので、\(K'(x)/K’\)も有限次拡大である。以上より拡大\(K'(x)/K\)が有限次拡大であることが分かり、特にこれは代数拡大である。よって\(x\)は\(K\)上代数的で、\(L/K\)が代数拡大なことが示された。
(2)\(x\in EF\)を任意に取る。定義から$$x=a_1b_1+\dots +a_nb_n\:\:(a_i\in E, b_i\in F)$$と表せる。ここで拡大体\(F’:=F(a_1,\dots ,a_n)\)を考えると、仮定から各\(a_i\)は\(K\)上代数的なので特に\(F\)上も代数的である。従って\(F’/F\)は代数拡大。上式から明らかに\(x\in F’\)なので、\(x\)は\(F\)上代数的。よって\(EF/K\)は代数拡大
(3)
(\(\Rightarrow\)) \(L=EF,M=E,F\)として(1)を適用すればよい。
(\(\Leftarrow\)) \(E/F\)は代数拡大なので(2)から\(EF/F\)は代数拡大。いま\(F/K\)も代数拡大なので(1)から\(EF/K\)は代数拡大である。
(証明終)




コメント