本記事では代数閉包の、準同型の拡張に関する性質について解説します。
主張
主張は以下の通りです。
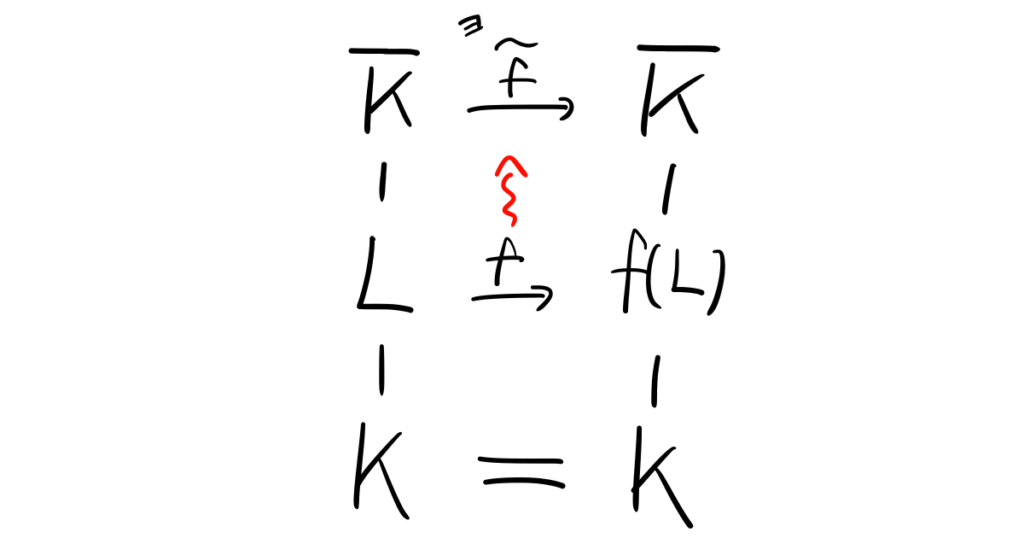
\(K\)を体、\(\overline K\)をその代数閉包、\(L\)を\(\overline K/K\)の中間体とする。
このとき、\(L\)から\(\overline K\)への\(K\)上の体準同型は\(\overline K\)の\(K\)上の自己同型に拡張できる。言い換えると、制限写像\[\text{Aut}(\overline K/K)\to \text{Hom}_K(L,\overline K);f\mapsto f|_L\]は全射となる。
図示すると以下の通りです。
証明
ツォルンの補題を使って証明します。
\(f\in \text{Hom}_K(L,\overline K)\)とする。\[\mathscr{L}:=\left\{ (M,g)\mid M:\overline K/Lの中間体, \;g\in \text{Hom}_K(M,\overline K),\;g|_L=f \right\} \]とおく。ここで\(\mathscr{L}\)に順序\(\leq\)を\[(M,g)\leq(N,h)\stackrel{\text{def}}{\Leftrightarrow} M\subset N,\;h|_M=g\]で定め、\(\mathscr{L’}\subset \mathscr{L}\)を全順序部分集合とする。このとき\[\widetilde L’:=\bigcup_{(M,g)\in \mathscr{L’}}M\]とし、写像\(\tilde f’ :\widetilde L’\to \overline K\)を\(x\in \widetilde L’\)に対し\(x\in M\)なる\((M,g)\in \mathscr{L’}\)を一つ取り、\[\tilde f'(x):=g(x)\]で定める。
(well-definedness)別の\(x\in M’\)なる\((M’,g’)\in \mathscr{L’}\)を取る。\(\mathscr{L’}\)は全順序集合なので、一般性を失わず\((M,g)\leq(M’,g’)\)としてよい。このとき\(g’|_M=g\)なので、\[g'(x)=g(x)\]となる。(証明終)
(\(\diamondsuit\))このとき\((\widetilde L’,\tilde f’)\in \mathscr{L}\)となり、さらにこれは\(\mathscr{L’}\)の上界となる。(証明は下部参照)
以上よりツォルンの補題から、\(\mathscr{L’}\)には極大元\((\widetilde L,\tilde f)\)が存在する。
以下\(\widetilde L=\overline K\)であることを示す。
\(\overline K\neq \widetilde L\)と仮定し、\(a\in \overline K\backslash \widetilde L\)を取り、\(a\)の\(\widetilde L\)上の最小多項式を\(F(X)\in \widetilde L[X]\)とする。\(\tilde f:\widetilde L\to \overline K\)は\(K\)上の同型\[
\widetilde L \stackrel{\cong}{\longrightarrow}\tilde f(\widetilde L)=:\widetilde L”
\]を誘導する。さらにこれが誘導する同型\(\widetilde L[X]\stackrel{\cong}{\longrightarrow} \widetilde L”[X]\)を同じく\(\tilde f\)と書くことにすると、\[F'(X):=\tilde f(F(X))\in \widetilde L”[X]\]は既約である(\(F(X)\)が既約なので)。\(F'(X)\)の根\(b\in \overline K\)を一つ取っておく。このとき代入写像\[\widetilde L”[X]\to \overline K ;h(X)\mapsto h(b)\]は\(\widetilde L”\)上の準同型\[\phi_b:\widetilde L”[X]/(F'(X))\to \overline K\]を誘導する。
さらに代入写像\(\widetilde L[X]\to \widetilde L(a)\)は\(\widetilde L\)上の体同型\[\phi_a:\widetilde L[X]/(F(X)) \stackrel{\cong}{\longrightarrow} \widetilde L(a)\]を誘導する。これらの合成\[\psi:\widetilde L(a)\stackrel{\phi_a^{-1}}{\longrightarrow}\widetilde L[X]/(F(X))\stackrel{\overline{\tilde f}}{\longrightarrow}\widetilde L”[X]/(F'(X))\stackrel{\phi_b}{\longrightarrow} \overline K\]は\(K\)上の準同型であり、\(\tilde f\)の拡張となっている。実際\(x\in \widetilde L\)に対し\begin{align}\psi(x)&=(\phi_b\circ \overline{\tilde f}\circ \phi_a^{-1})(x)\\[5pt]&=(\phi_b\circ \overline{\tilde f})(x)\quad(\phi_a^{-1}は\widetilde L上の同型)\\[5pt]&=\phi_b(\tilde f(x))\\[5pt]&=\tilde g(x)\quad(\phi_bは\widetilde L”=\text{Im} \tilde f上の準同型)
\end{align}が成立する。いま\(a\notin \widetilde L\)より\[(\widetilde L,\tilde f)<(\widetilde L(a),\psi)\]となるが、これは\((\widetilde L,\tilde f)\)の極大性に矛盾。よって\(\widetilde L=\overline K\)である。
以上より\(\tilde f\)は\(\overline K\)の\(K\)上の自己準同型である。あとはこれが全射であることを示せばよい。そうでないと仮定し、\(c\in \overline K\backslash \tilde f(\overline K)\)を取る。\(c\)の\(K\)上の最小多項式を\(f_c(X)\in K[X]\)とする。これを\(\overline K[X]\)において\[f_c(X)=(X-c_1)\cdots(X-c_n)\qquad(c_i\in \overline K)\]と分解し、この両辺の\(\tilde f\)による像を考えると\(\tilde f\)が\(K\)上の同型であることから\[f_c(X)=(X-\tilde f(c_1))\cdots(X-\tilde f(c_n))\]となる。いま\(f_c(c)=0\)よりある\(i\)に対し\(\tilde f(c_i)=c\)となるが、これは\(c\in \overline K\backslash \tilde f(\overline K)\)に矛盾。よって\(\tilde f\)は全射である。
以上より、\(\tilde f\)は\(f\)の拡張となる\(\text{Aut}(\overline K/K)\)の元である。
(証明終)
\(\diamondsuit\)の証明
\(a,b\in \widetilde L’\)とすると、それぞれ\(a\in M_a,b\in M_b\)なる\((M_a,g_a),(M_b,g_b)\in \mathscr {L’}\)がある。\(\mathscr{L’}\)は全順序集合なので一般性を失わず\(M_a\subset M_b\)としてよい。このとき\(a,b\in M_b\)より\[a-b,ab\in M_b\subset \widetilde L’\]となる。同様にして\(0\neq a\in \widetilde L’\)に対し\(a^{-1}\in \widetilde L’\)が示せるので\(\widetilde L’\)は体となる。
\(\tilde f’\)が\(f\)の拡張となるのは定義から明らか(定義に使った\(g\)がそもそも\(f\)の拡張なので)。よって\((\widetilde L’,\tilde f’)\in \mathscr{L}\)となる。
\((M,g)\in \mathscr{L’}\)とすると、定義から\(M\subset \widetilde L’\)となる。よって\(\tilde f’\)の定義から\(x\in M\)に対し\(\tilde f'(x)=g(x)\)となるので、\(\tilde f’|_M=g\)となる。したがって\((M,g)\leq (\tilde L’,\tilde f’)\)となる。
以上より\((\tilde L’,\tilde f’)\)は\(\mathscr{L’}\)の上界である。
(証明終)
やはりツォルンの補題は強いですね。
応用
よく使われる系は次のような場合です。
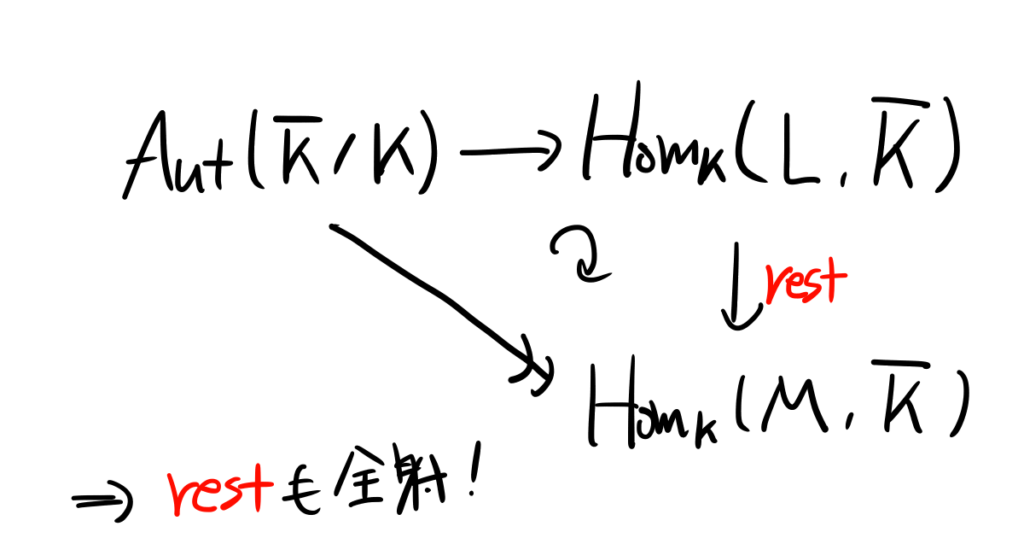
\(L/M/K\)を代数拡大の列とする。このとき\(M\)から\(\overline K\)への\(K\)上の体準同型は、\(L\)へと拡張できる。言い換えれば制限写像\[\text{Hom}_K(L,\overline K)\to \text{Hom}_K(M,\overline K);f\mapsto f|_M\]は全射である。
(証明)\(L/M/K\)が代数拡大であることから、\(\overline L=\overline M =\overline K\)である。制限写像の合成\[\text{Aut}(\overline K/K)\to\text{Hom}_K(L,\overline K)\to \text{Hom}_K(M,\overline K)\]は制限写像\[\text{Aut}(\overline K/K)\to \text{Hom}_K(M,\overline K)\]に他ならず、上で示したことよりこれは全射である。従って特に\[\text{Hom}_K(L,\overline K)\to \text{Hom}_K(M,\overline K)\]は全射である。



コメント