本記事では、局所化の推移性について解説します。
主張
主張は以下の通りです。
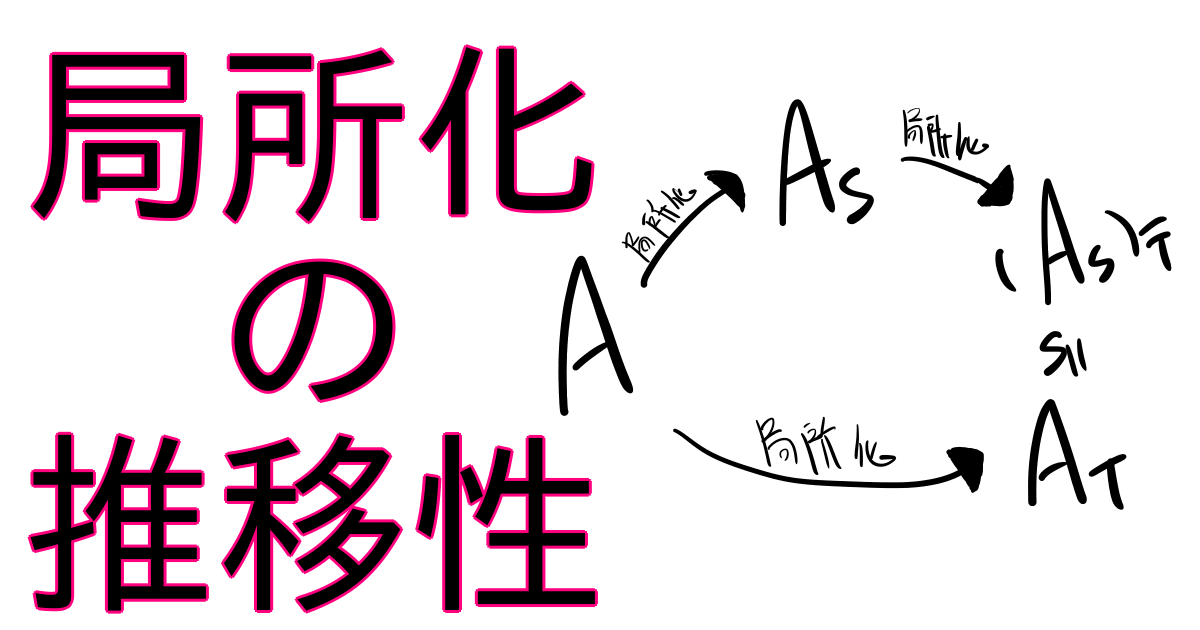
\(A\)を可換環、\(S,T\subset A\)を\(S\subset T\)なる積閉集合とする。このとき以下が成り立つ。$$A_T\cong (A_S)_{\overline{T}}$$ただし\(\overline{T}\)とは自然な準同型\(A\to A_S\)による\(T\)の像のこととする。
大雑把に言うと、「小さい\(S\)で局所化してから大きい\(T\)で局所化する」ことと「初めから大きい\(T\)で局所化する」ことは同じだということです。
局所化って何だっけ?という方は、以下の記事で解説しているのでぜひご覧ください。
証明
愚直に環準同型を構成し、それが全単射であることをチェックします。
まず自然な準同型\(i:A\to A_T\)を考える。\(S\subset T\)より、任意の\(s\in S\)に対し、$$i(s)=\frac{s}{1}\in A_T^{\times}$$となる。よって局所化の普遍性より、\(i\)は環準同型$$i’:A_S\to A_T\;;\;\frac{a}{b}\mapsto \frac{a}{b}$$を誘導する。さらに\(a/b\in\overline{T}\:\)とすると、\(a\in T\)であることから$$i’\left(\frac{a}{b}\right)=\frac{a}{b}\in A_T^{\times}$$となるので、\(i’\)はさらに環準同型$$f:(A_S)_{\overline{T}}\to A_T\;;\;\frac{\frac{a}{b}}{\frac{c}{d}}\mapsto \frac{a}{b}\cdot\left(\frac{c}{d}\right)^{-1}=\frac{ad}{bc}$$を誘導する。これが全単射であることをみる。
(単射性) \(\mathrm{ker}f=\{0\}\)を示せばよいので、$$f\left(\frac{\frac{a}{b}}{\frac{c}{d}}\right)=\frac{ad}{bc}=0 \in A_T$$と仮定する。この時局所化の定義より、ある\(t\in T\)が存在し、$$tad=0\in A$$となる。いま\(d\in S\)なので局所化の定義から$$\frac{ta}{b}=0\in A_S$$となる。これはすなわち$$\frac{t}{1}\cdot\frac{a}{b}=0\in A_S$$ということであり、\(t/1\in \overline{T}\)より結局、$$\frac{\frac{a}{b}}{\frac{c}{d}}=0\in (A_S)_{\overline{T}}$$が従う。よって\(f\)は単射。
(全射性) \(a/b\in A_T\)を任意に取る。このとき\(b\in T\)より\(b/1\in \overline{T}\)である。ここで定義から明らかに$$f\left(\frac{\frac{a}{1}}{\frac{b}{1}}\right)=\frac{a}{b}$$なので\(f\)は全射。
以上より\(f\)は同型。
(証明終)
局所化を考えるときはどこの世界でゼロなのかを意識する必要があるのでちょっとややこしいですね。
特別な場合
素イデアルによる局所化の場合を考えてみましょう。
\(p,q\subset A\)を\(q\subset p\)なる素イデアルとする。この時、\(S=A\,\backslash\, p,T=A\,\backslash\, q\)として上の性質を適用すると、以下を得る。$$ A_q\cong (A_p)_{qA_p}$$
これは代数多様体の滑らかさの判定に関係してくるので、地味に重要な性質です。


コメント