本記事では正規拡大の中間体に関する性質について解説します。
主張
主張は以下の通りです。
\(L/K\)を体の拡大、\(M,E,F\)をその中間体とし、\(EF\)を\(E\)と\(F\)の合成体とする。このとき以下が成立する。\begin{align}&(1)\;L/K\text{は正規拡大}\Rightarrow L/M\text{は正規拡大}\\[10pt]&(2)\;E/K\text{は正規拡大}\Rightarrow EF/F\text{は正規拡大}\\[10pt]&(3)\;E/K,F/K\text{は正規拡大}\Rightarrow EF/K\text{は正規拡大}\end{align}
図示すると以下の通りです。
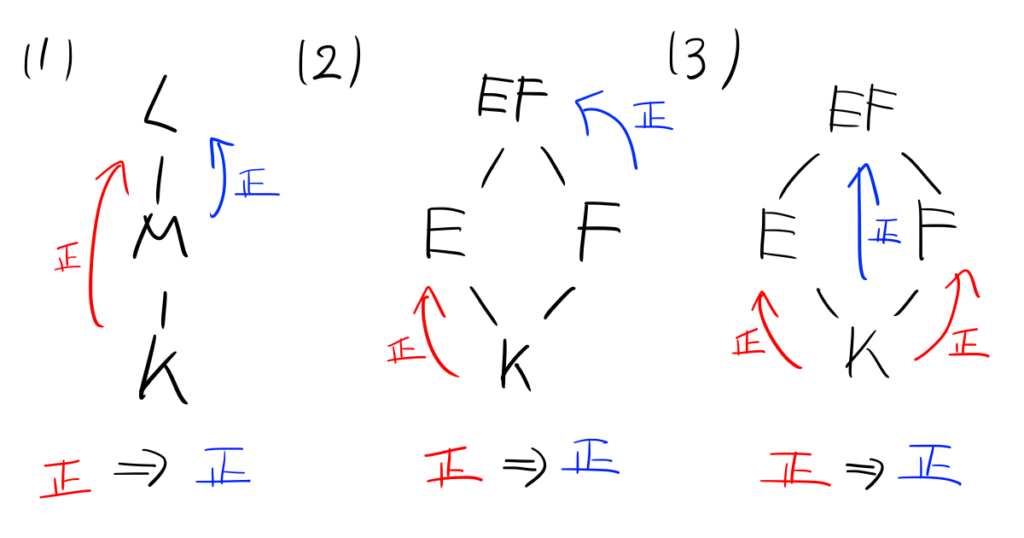
全体的に分離拡大や代数拡大より弱くなっていますね。
証明
準同型に関する正規拡大の特徴付けを使って証明します。詳しくは以下の記事もご覧ください。
\((1)\)\(\phi\in \text{Hom}_M(L,\overline M)\)とする。\(M/K\)は代数拡大なので\(\overline M=\overline K\)となる。また\(K\subset M\)より\[\phi|_K=\text{id}\]となるので、\[\phi\in \text{Hom}_K(L,\overline K)\]でもある。いま\(L/K\)は正規拡大なので\[\phi(L)\subset L\]となる。これより\(M/K\)は正規拡大である。
\((2)\)\(\phi \in\text{Hom}_F(EF,\overline F)\)とする。上と同様の理由から\[\phi|_E\in \text{Hom}_K(E,\overline F)=\text{Hom}_K(E,\overline K)\]となる。いま\(E/K\)は正規拡大なので\[\phi(E)\subset E\]となる。また\(\phi|_F=\text{id}\)ゆえ明らかに\[\phi(F)= F\]となる。したがって\[\phi(EF)=\phi(E)\phi(F)\subset EF\]となる。従って\(EF/F\)は正規拡大。
\((3)\)\(\phi\in \text{Hom}_K(EF,\overline K)\)とする。\[\phi|_E \in \text{Hom}_K(E,\overline K),\phi|_F\in \text{Hom}_K(F,\overline K)\]となり、\(E/K,F/K\)が正規拡大であることから\[\phi(E)\subset E,\phi(F)\subset F\]が成立する。従って\[\phi(EF)=\phi(E)\phi(F)\subset EF\]となり、\(EF/K\)は正規拡大である。
(証明終)
反例
冒頭でも述べた通り、今回紹介する性質は分離拡大などより弱いものとなっています。弱まるにあたって落とされた主張について、いくつか反例を見ておきましょう。
\((1)\)に関する反例
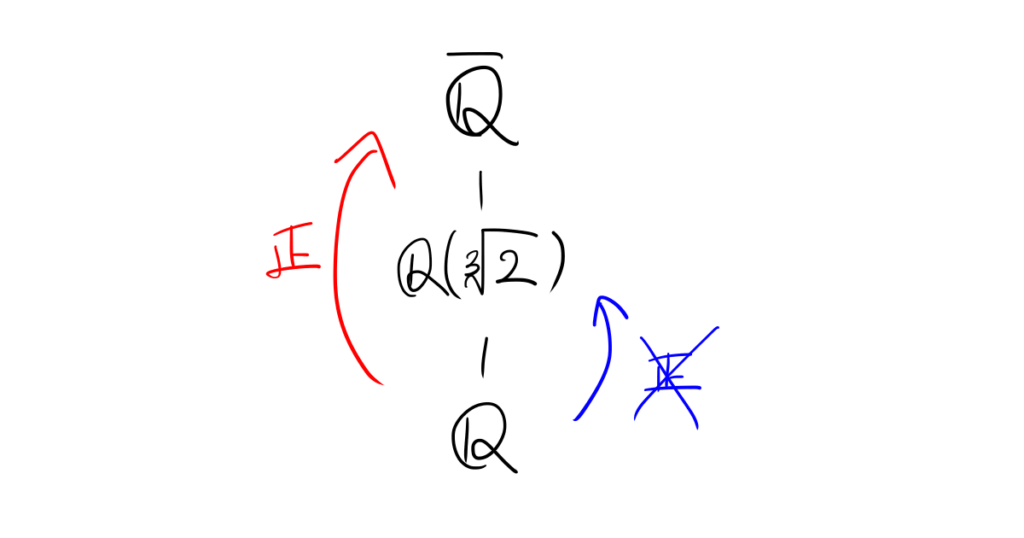
拡大\(\overline {\mathbb{Q}}/\mathbb{Q}(\sqrt[3]2)/\mathbb{Q}\)を考えてみましょう。\(\overline {\mathbb{Q}}\)は\(\mathbb{Q}\)の代数閉包なので\(\overline {\mathbb{Q}}/\mathbb{Q}\)は正規拡大です。
ここで\(\mathbb{Q}(\sqrt[3]2)/\mathbb{Q}\)についてみてみましょう。\(\sqrt[3]2\)の\(\mathbb{Q}\)上の最小多項式は\[X^3-2\]です。これは\(\mathbb{C}[X]\)において\[(X-\sqrt[3]2)(X-\omega\sqrt[3]2)(X-\omega^2\sqrt[3]2)\qquad(\omega:=\frac{-1+i\sqrt3}{2})\]と分解できます。従って\(\sqrt[3]2\)の\(\mathbb{Q}\)上の共役元は\(\sqrt[3]2,\omega\sqrt[3]2,\omega^2\sqrt[3]2\)の3つだと分かります。
ここで\(\omega\sqrt[3]2,\omega^2\sqrt[3]2\)は実数ではないので、\[\omega\sqrt[3]2,\omega^2\sqrt[3]2\notin \mathbb{Q}(\sqrt[3]2)\]となります。従って\(\mathbb{Q}(\sqrt[3]2)/\mathbb{Q}\)は正規拡大ではありません。
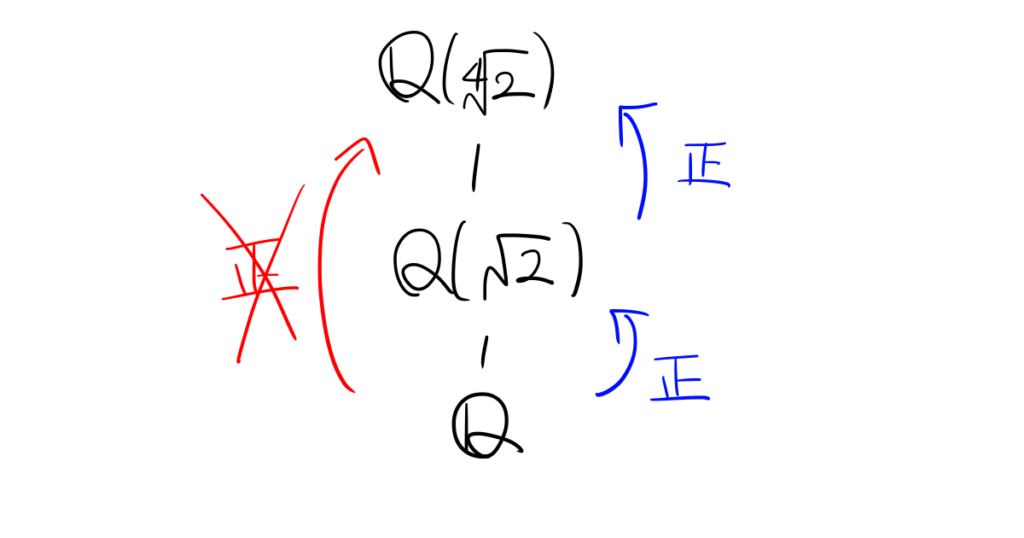
次に\(\mathbb{Q}(\sqrt[4]2)/\mathbb{Q}(\sqrt2)/\mathbb{Q}\)という拡大を考えます。\(\sqrt2\)の\(\mathbb{Q}\)上の共役元はもちろん\(-\sqrt2\)であり、これは\(\mathbb{Q}(\sqrt2)\)の元なので\(\mathbb{Q}(\sqrt2)/\mathbb{Q}\)は正規拡大です。
また\(\sqrt[4]2\)の\(\mathbb{Q}(\sqrt2)\)上の最小多項式は\[X^2-\sqrt2\]で与えられるので、\(\sqrt[4]2\)の\(\mathbb{Q}(\sqrt2)\)上の共役元は\(-\sqrt[4]2\)であり、これは\(\mathbb{Q}(\sqrt[4]2)\)の元です。従って\(\mathbb{Q}(\sqrt[4]2)/\mathbb{Q}(\sqrt2)\)も正規拡大です。
しかし\(\mathbb{Q}(\sqrt[4]2)/\mathbb{Q}\)に着目すると、\(\sqrt[4]2\)の\(\mathbb{Q}\)上の最小多項式は\[X^4-2\]であり、これの根には\(\sqrt[4]{2}i\)がある。これは明らかに実数ではないので、\[\sqrt[4]{2}i\notin\mathbb{Q}(\sqrt[4]2)\]となり、\(\mathbb{Q}(\sqrt[4]2)/\mathbb{Q}\)が正規拡大でないことが分かります。
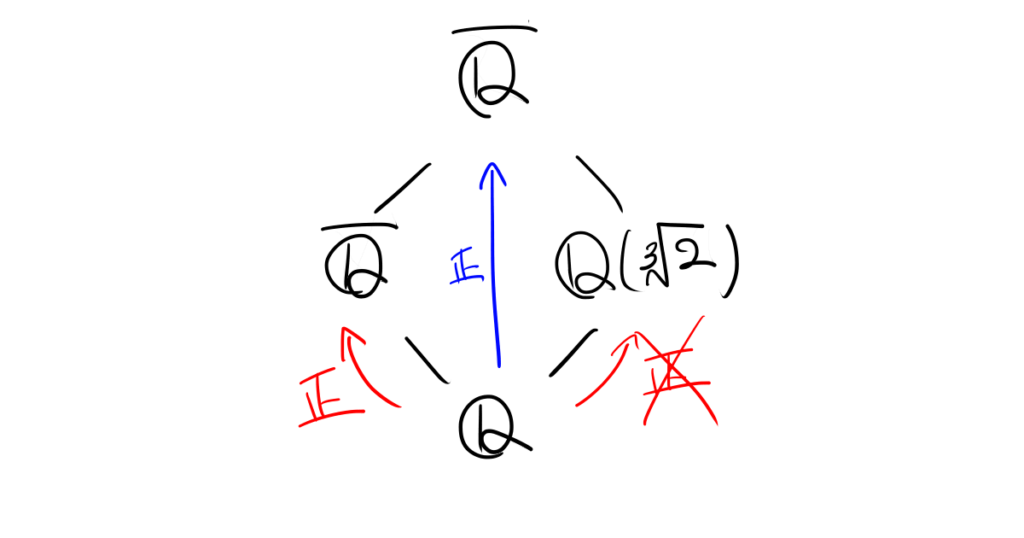
\((3)\)に関する反例
\(K=\mathbb{Q},E=\mathbb{Q}(\sqrt[3]2) ,F=\overline{\mathbb{Q}}\)とすれば、\[EF=\overline{\mathbb{Q}}\]なので\(EF/K\)は正規拡大ですが、上で見たように\(E/K\)は正規拡大ではありません。
あまり面白くはないですが、これが逆方向の反例になります。(ちなみにこれは(\(2)\)の逆の反例にもなっています)




コメント