本記事ではガロア理論の推進定理について解説します。
前提
本記事では以下の内容を前提としています。それぞれ詳細はリンク先の記事をご覧ください。
\(L/K\)を体の拡大、\(E,F\)をその中間体とし、\(EF\)を\(E\)と\(F\)の合成体とする。このとき以下が成立する。\begin{equation}\begin{split}&(1)\;E/K\text{はガロア拡大}\Rightarrow EF/F\text{はガロア拡大}\\[10pt]&(2)\;E/K,F/K\text{はガロア拡大}\Rightarrow EF/K\text{はガロア拡大}\end{split}\tag{$\color{red}{\star}$}\end{equation}
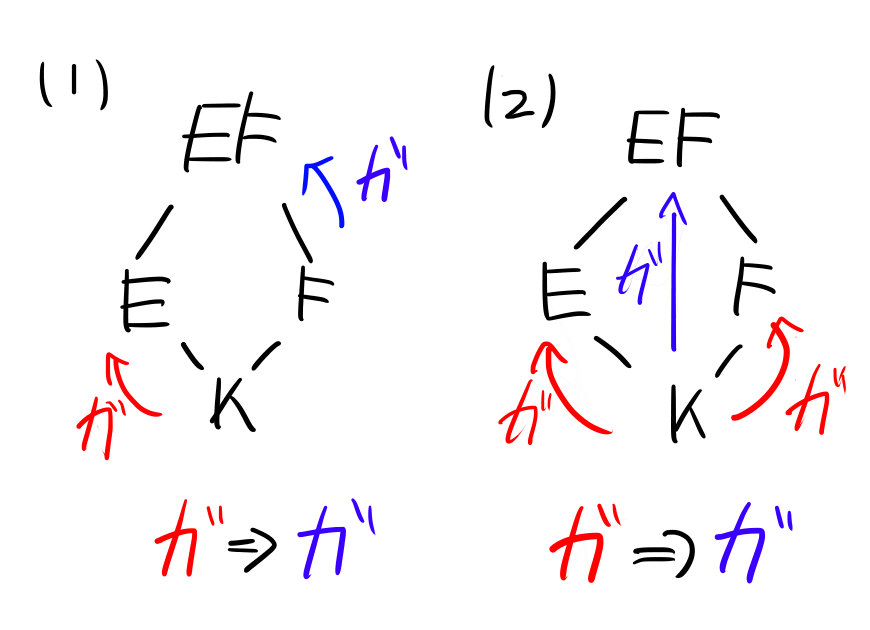
\(L/K\)を有限次ガロア拡大とする。このとき\(L/K\)の中間体と、ガロア群 \(G:=\mathrm{Gal}(L/K)\)の部分群は以下の対応により一対一に対応している。\begin{align}
L\supset M &\mapsto \mathrm{Gal}(L/M) \subset G \\[10pt]
G \supset H &\mapsto L^H \subset L \end{align}
これらを踏まえて、まずは推進定理でどのようなことを考えるのかを見ていきましょう。
気持ち
ガロア理論の基本定理により、有限次ガロア拡大の中間体とガロア群の部分群には一対一対応がありました。しかもただ対応しているだけでなく、包含関係や合成などの情報も保った非常に良い対応です。
つまりガロア群は、ガロア拡大に関し非常に多くの情報を保持しているということです。
ところで上にあるガロア拡大の性質 (\(\color{red}{\star}\)) によると、2つの中間体 \(E,F\)に対し、拡大
\[E/E\cap F\;\text{と}\; EF/F, \]\[
E/E\cap F\,,\, F/E\cap F\,\text{と}\,EF/E\cap F\]にはガロア拡大について関係があることが分かります。
ということは、(これらがガロア拡大になるときには)対応するガロア群にも何らかの関係があるのではないか……？というのが今回紹介する推進定理の内容になります。
主張
主張は以下の通りです。
\(L/K\)を体の拡大、\(E,F\)をその中間体とすると、以下が成立する。\[(1)\,
E/E\cap F\,\text{は有限次ガロア拡大}\Rightarrow EF/F\,\text{は有限次ガロア拡大}\]となり、さらにこのとき\[
\color{red}{\mathrm{Gal}(EF/F) \cong \mathrm{Gal}(E/E\cap F)} \]が成立する。
\[(2)\,
E/E\cap F\,,\,F/E\cap F\,\text{は有限次ガロア拡大}\Rightarrow EF/E\cap F\,\text{は有限次ガロア拡大}\]となり、さらにこのとき\[\color{red}{
\mathrm{Gal}(EF/E\cap F) \cong \mathrm{Gal}(E/E\cap F)\times \mathrm{Gal}(F/E\cap F) }\]が成立する。
(証明) (\(1\))性質(\(\color{red}{\star}\)) から \(EF/F\)はガロア拡大である。また \(E/E\cap F\) は有限次拡大なので、ある \(E \cap F \) 上代数的な元 \(a_1,\dots,a_n\in E\) が存在し、\[
E=(E\cap F)(a_1,\dots,a_n)\]が成立する。これより\[
EF=F(E)=F(E\cap F,a_1,\dots,a_n)=F(a_1,\dots,a_n)\]となるが、\(a_1,\dots,a_n\) は\(E\cap F\)上代数的より、特に\(F\)上代数的なので \(EF/F\) は有限次拡大である。
また、\(f\in\mathrm{Gal}(EF/F)\) に対し \(f|_E\) を考えると、\(E/E\cap F\) が正規拡大であることから、\[f(E)\subset E\]となる(\(\because\) 正規拡大の性質)。よって \(f|_E\) は\(\mathrm{Gal}(E/E\cap F)\) の元となり、準同型\[\Phi:
\mathrm{Gal}(EF/F)\to\mathrm{Gal}(E/E\cap F)\,;\,f\mapsto f|_E\]が定まる。
(単射性) \(f\in\mathrm{Gal}(EF/F)\) が\[f|_E=\mathrm{id}_E\]を満たしたとする。これはすなわち \(f\) は \(E\) の元を固定するということ。よって \(f\) は \(E,F\) の元を共に固定するので、\[
f=\mathrm{id}_{EF}\]が従う。よって\(\Phi\) は単射である。
(全射性) \[G:=\mathrm{Im}(\Phi)\]とおく。\(G\) は \(\mathrm{Gal}(E/E\cap F)\) の部分群なので、有限次ガロア拡大 \(E/E\cap F\) に関するガロア理論の基本定理から\[
E^G=E\cap F\]を示せば、\(G=\mathrm{Gal}(E/E\cap F)\) すなわち \(\Phi\) が全射であることが従う。
\(x\in E^G\) とする。このとき任意の \(f\in\mathrm{Gal}(EF/F)\) に対し\[
f(x) = f|_E(x) =x\quad(\because\,x\in E^G)\]より有限次ガロア拡大 \(EF/F\) に関するガロア理論の基本定理から\[x\in EF^{\mathrm{Gal}(EF/F)}=F\]が従う。よって \(x\in E\cap F\) となり、\(E^G=E\cap F\) が従い\(\Phi\) が全射であることが示された。
以上により \(\Phi\) は同型である。
(\(2\)) 性質(\(\color{red}{\star}\)) から \(EF/E\cap F\) はガロア拡大である。また(\(1\))より \[
[EF:E\cap F]={\color{red}{[EF:F]}} [F:E\cap F]={\color{red}{[E:E\cap F]}}[F:E\cap F]<\infty\]より \(EF/E\cap F\) は有限次拡大である。
さらに先と同様に準同型\[\Psi:
\mathrm{Gal}(EF/E\cap F)\to\mathrm{Gal}(E/E\cap F)\times\mathrm{Gal}(EF/E\cap F)\,;\,f\mapsto (f|_E,f|_F)\]を考える。これが単射であることを示すため、\(f\in \mathrm{Gal}(EF/E\cap F)\) が\[
f|_E=\mathrm{id}_E\,,\,f|_F=\mathrm{id}_F\]を満たしたとすると、\(f\) は \(E,F\) の元を共に固定するので、\(f=\mathrm{id}_{EF}\) が従う。よって \(\Psi\) は単射であり、いま\[
|\mathrm{Gal}(EF/E\cap F)|=|\mathrm{Gal}(E/E\cap F)\times\mathrm{Gal}(EF/E\cap F)|\]なので \(\Psi\) は同型となる。
名前といい主張といいかなり好きな定理です。
コメント